Tales de Mileto
Tales de Mileto fue un filósofo, matemático, geómetra, físico y legislador griego. Fue el iniciador de la Escuela de Mileto a la que pertenecieron también Anaximandro (su discípulo) y Anaxímenes (discípulo del anterior). En la antigüedad se le consideraba uno de los Siete Sabios de Grecia. No se conserva ningún texto suyo y es probable que no dejara ningún escrito a su muerte. Desde el siglo V a. C. se le atribuyen importantes aportaciones en el terreno de la filosofía, la matemática, la astronomía, la física, etc., así como un activo papel como legislador en su ciudad natal.
Se suele aceptar que Tales comenzó a usar el pensamiento deductivo aplicado a la geometría, y se le atribuye la enunciación de dos teoremas geométricos que llevan su nombre.
Teorema de Tales
Existen dos teoremas relacionados con la geometría clásica que reciben el nombre de teorema de Tales:
El primero de ellos explica esencialmente una forma de construir un triángulo semejante a uno previamente existente ("los triángulos semejantes son los que tienen ángulos iguales y sus lados homólogos proporcionales"). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos ("encontrándose estos en el punto medio de su hipotenusa"), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersectadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales.
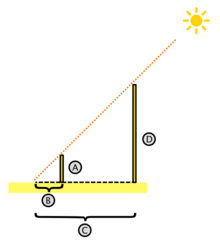
Teorema primero
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.
Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo.
Sea B un punto de la circunferencia de diámetro AC, distinto de Ay de C. Entonces el triángulo ABC, es un triángulo rectángulo.
El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos.

Demostración:
En la circunferencia de centro O y radio r (véase fig 2.3), los segmentos
-
- OA , OB y OC
son iguales por ser todos radios de la misma circunferencia.
Por lo tanto los triángulos AOB y BOC son isósceles.
La suma de los ángulos del triángulo ABC es:
Dividiendo ambos miembros de la ecuación anterior por dos, se obtiene:
-
- -Andrada Ioana Ursarescu





No hay comentarios:
Publicar un comentario